Computational Physics (Part 3)

[TOC]

7. Fourier Transform

7.1 Fourier Transform

Definition:

$\begin{aligned} & H(f)=\int_{-\infty}^{\infty} h(t) e^{2 \pi i f t} d t \\ & h(t)=\int_{-\infty}^{\infty} H(f) e^{-2 \pi i f t} d f \end{aligned}$

Convolution Theorem:

$g * h \equiv \int_{-\infty}^{\infty} g(\tau) h(t-\tau) d \tau \Leftrightarrow G(f) H(f)$

Parseval Theorem:

$\int_{-\infty}^{\infty}|h(t)|^2 d t=\int_{-\infty}^{\infty}|H(f)|^2 d f$

7.2 Discrete Fourier transform (DFT)

Basic idea: We use discrete points in the time domain to compute discrete points in the frequency domain

Time domain:

$h_k=h\left(t_k\right), t_k=k \Delta, \quad k=1,2, \ldots, N-1$

Freq domain:

$f_n=\frac{n}{N \Delta}, n=-\frac{N}{2}, \ldots, \frac{N}{2}$

Then the generic form of DFT is

$H\left(f_n\right)=\int_{-\infty}^{\infty} h(t) e^{2 \pi i f_n t} d t \approx \sum_{k=0} h_k e^{2 \pi i f_n t_k} \Delta=\Delta \sum_{k=0} h_k e^{2 \pi i k n / N}$

define

$H_n=\sum_{n=0}^{N-1} h_k e^{2 \pi i k n / N}$

Finally we have

$H(f_n)\approx \Delta H_n$

Inverse Fourier transform

$h_k = \frac{1}{N}\sum_{n=0}^{N-1}H_n e^{-2\pi ikn/N}$

Parseval’s theorem in discrete form

$\sum_{k=0}^{N-1}\left|h_k\right|^2=\frac{1}{N} \sum_{n=0}^{N-1}\left|H_n\right|^2$

and the corresponding convolution

$(r * s)_j \equiv \sum_{k=-\frac{M}{2}+1}^{\frac{M}{2}} s_{j-k} r_k \Leftrightarrow S_n R_n$

7.3 Fast Fourier Transform (FFT)

7.3.1 Generic From

The principle of the fast Fourier transform comes from Danielson and Lanczos’ discovery of the equivalent transformation, that is, the Fourier transform of a discrete sequence of length 𝑁 can be written as the sum of the Fourier transforms of two discrete sequences of length 𝑁/2, where the two half-length sequences correspond to odd lattice points and even lattice points of the original sequence.

$\begin{gathered} F_k=\sum_{j=0}^{N-1} e^{\frac{2 \pi i j k}{N}} f_j=\sum_{j=0}^{\frac{N}{2}-1} e^{\frac{2 \pi i(2 j) k}{N}} f_{2 j}+\sum_{j=0}^{\frac{N}{2}-1} e^{\frac{2 \pi i(2 j+1) k}{N}} f_{2 j+1} \\ F_k=\sum_{j=0}^{\frac{N}{2}-1} e^{\frac{2 \pi i j k}{N / 2}} f_{2 j}+W^k \sum_{j=0}^{\frac{N}{2}-1} e^{\frac{2 \pi i j k}{N / 2}} f_{2 j+1}=F_k^e+W^k F_k^o \end{gathered}$

where

$W=e^{2\pi i/N}$

In the other hand, we can show easily

$F_{k+N/2} = F_k^e-W^kF_k^o$

In the specific iteration process, we can use a list with size to realize the iteration. the only thing we need to do is pay attention to the rank of the list.

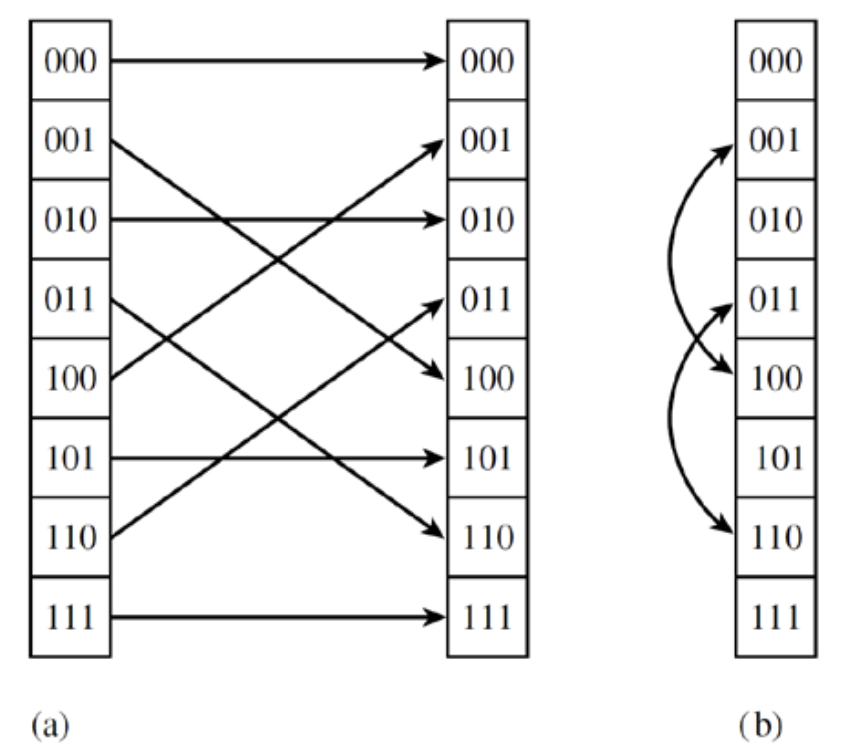
We can also use series decomposition method to increase the efficiency of the iteration

Suppose

$N = m \times M$

and are both the power of 2. Then we have

$F[k M+K]=\sum_j\left\{e^{2 \pi i j k / m}\left[e^{\frac{2 \pi i j K}{M m}}\left(\sum_J e^{\frac{2 \pi i j K}{M}} f(J m+j)\right)\right]\right\}$

which means we can calculate transformation of first and then for the . It can be accelerated with the parallel computing.

Since generically the function in time domain is real but the Fourier transformation is in the complex domain, we can accelerate the calculation by combine two set of data. Namely,

$H_n=\sum_j e^{\frac{2 \pi i j n}{N}}\left(f_j+i g_j\right)=F_n+i G_n$

and

$\left(H_{N-n}\right)^*=\left(\sum_j e^{\frac{2 \pi i j(N-n)}{N}}\left(f_j+i g_j\right)\right)^*=\sum_{\mathrm{j}} e^{\frac{2 \pi i j n}{N}}\left(f_j-i g_j\right)=F_n-i G_n$

Also we can choose

$h_j=f_{2 j}+i f_{2 j+1} \quad j=0, \ldots, \frac{N}{2}-1$

7.3.2 Sine & Cosine Transform

First Method:

construct a odd function

$f_{2 N-j}=-f_j \quad j=0, \ldots, N-1$

and do the FFT

$F_k=\sum_{j=0}^{N-1} f_j\left[e^{\frac{2 \pi i j k}{2 N}}-e^{-\frac{2 \pi i j k}{2 N}}\right]=2 i \sum_{j=0}^{N-1} f_j \sin \left(\frac{\pi j k}{N}\right)$

Another Method:

$\begin{gathered} y_0=0 \\ y_j=\sin \left(\frac{j \pi}{N}\right)\left(f_j+f_{N-j}\right)+\frac{1}{2}\left(f_j-f_{N-j}\right) \quad j=1, \ldots, N-1 \end{gathered}$

And do the real Fourier transform

$\begin{gathered} R_k=\sum_{j=0}^{N-1} y_j \cos \left(\frac{2 \pi j k}{N}\right)=\sum_{j=1}^{N-1}\left(f_j+f_{N-1}\right) \sin \left(\frac{j \pi}{N}\right) \cos \left(\frac{2 \pi j k}{N}\right)=\sum_{j=0}^{N-1} 2 f_j \sin \left(\frac{j \pi}{N}\right) \cos \left(\frac{2 \pi j k}{N}\right) \\ =\sum_{j=0}^{N-1} f_j\left[\sin \frac{(2 k+1) j \pi}{N}-\sin \frac{(2 k-1) j \pi}{N}\right]=F_{2 k+1}-F_{2 k-1} \\ I_k=\sum_{j=0}^{N-1} y_j \sin \left(\frac{2 \pi j k}{N}\right)=\sum_{\mathrm{j}=1}^{N-1}\left(f_j-f_{N-j}\right) \frac{1}{2} \sin \left(\frac{2 \pi j k}{N}\right)=\sum_{j=0}^{N-1} f_j \sin \left(\frac{2 \pi j k}{N}\right)=F_{2 k} \end{gathered}$

Finally obtain

$\begin{gathered} F_{2 k}=I_k \quad k=0, \ldots,\left(\frac{N}{2}-1\right) \\ F_{2 k+1}=F_{2 k-1}+R_k \quad k=0, \ldots,\left(\frac{N}{2}-1\right) \end{gathered}$

7.4 Fourier Integral

Basic idea: using the interpolation method and FFT to calculate the integral.

Integral:

$I=\int_a^b e^{i \omega t} h(t) d t$

Interpolation:

$h(t) \approx \sum_{j=0}^M h_j \psi\left(\frac{t-t_j}{a}\right)+\sum_{j=\text { boundary }} h_j \phi_j\left(\frac{t-t_j}{\Delta}\right)$

FFT:

$I \approx \Delta e^{i \omega a}\left[W(\theta) \sum_j^M h_j e^{i j \theta}+\sum_{j=\text { boundary }} h_j \alpha_j(\theta)\right]$

where and

$\begin{gathered} W(\theta)=\int_{-\infty}^{+\infty} d s e^{i \theta s} \psi(s) \\ \alpha_j(\theta)=\int_{-\infty}^{+\infty} d s e^{i \theta s} \phi_j(s-j) \end{gathered}$

7.5 Nonequal Interval Spectrum Analysis

Basic idea: use the interpolation method to construct a unit interval time domain dataset.

7.5.1 Lomb Method

Lomb gives a estimation of Periodogram

$P_N(\omega)=\frac{1}{2 \sigma^2}\left\{\frac{\left[\sum_j\left(h_j-\bar{h}\right) \cos \omega\left(t_j-\tau\right)\right]^2}{\sum_j \cos ^2 \omega\left(t_j-\tau\right)}+\frac{\left[\sum_j\left(h_j-\bar{h}\right) \sin \omega\left(t_j-\tau\right)\right]^2}{\sum_j \sin ^2 \omega\left(t_j-\tau\right)}\right\}$

where

$\tan (2 \omega \tau)=\frac{\sum_{\mathrm{j}} \sin 2 \omega t_j}{\sum_{\mathrm{j}} \cos 2 \omega t_j}$