原子分子碰撞中的time delay（一）

1.引言

激光技术的快速进展使得我们能够在原子和分子的自然超快时间尺度上探测电子动力学。在理解超快过程的理论框架中，量子碰撞理论中的“Wigner time delay”被视为一个重要的方法。多年来，关于量子碰撞现象中的time delay已有大量的研究。本文旨在初步介绍“Wigner time delay”。（本文主要参考文献Deshmukh, P. C., & Banerjee, S. (2020). Time delay in atomic and molecular collisions and photoionisation/photodetachment. International Reviews in Physical Chemistry, 40(1), 127–153. https://doi.org/10.1080/0144235X.2021.1838805）

在经典物理学中，时间与能量一起作为一对正则共轭变量可以在哈密顿-雅可比理论中进行正则变换。然而，在量子理论里，时间与其他相空间变量之间有着本质的区别，即使能量和时间之间看似可以写成类似于海森堡位置-动量不确定性之间的关系。我们仍然认为时间是一个经典的参量，它无法被量子化也没有像位置和动量那样的量子算符（即使能量的算符是众所周知的哈密顿算符）。特别地，海森堡位置-动量之间的不确定关系：

$\delta p \delta q \geq \hbar / 2,$

中的和是使用适当的位置和动量算符定义的统计均方根偏差。而能量和时间之间的不确定性关系为：

$\delta E \delta t \geq \hbar / 2,$

其形式与上述位置和动量的不确定性相同，但其本质上是不同的，位置和动量的不确定性关系是利用自伴算符的性质得到的，而能量和时间的不确定性关系则是通过傅里叶变换得到的。

由于哈密顿算符与能量相关并且它的谱具有下界，因此不可能将算符与时间相关联。这个问题可以进一步通过 Stone–von Neumann 定理来讨论。因此，即便“时间”本身不是可观测量、无法通过厄米算符表示，我们仍然可以定义一个”时间延迟”，它是一个可观测量。时间延迟是可测量的，且可以用一个自伴的量子算符来表征这一特性，我们将在下面这一节详细讲一下我们是如何引入”时间延迟”的。

2.Wigner-Eisenbud 时间延迟

众所周知，当一个入射粒子波函数与散射势相互作用时，其波函数会发生相移。这个相移包含了关于入射粒子与目标势相互作用的所有信息。入射粒子束由于不是严格的单色波，我们可以用具有某个平均动量的平面波的叠加波包来表示。波包以群速度传播，而波包中的每个单独波以相速度传播。相速度的频率依赖性会导致波包随着时间的推移而扩散。我们考虑一个粒子波包与中心场势的散射问题。由于势具有对称性，我们可以使用球坐标系将球谐函数从径向波函数中分离。下图展示了问题的径向部分。

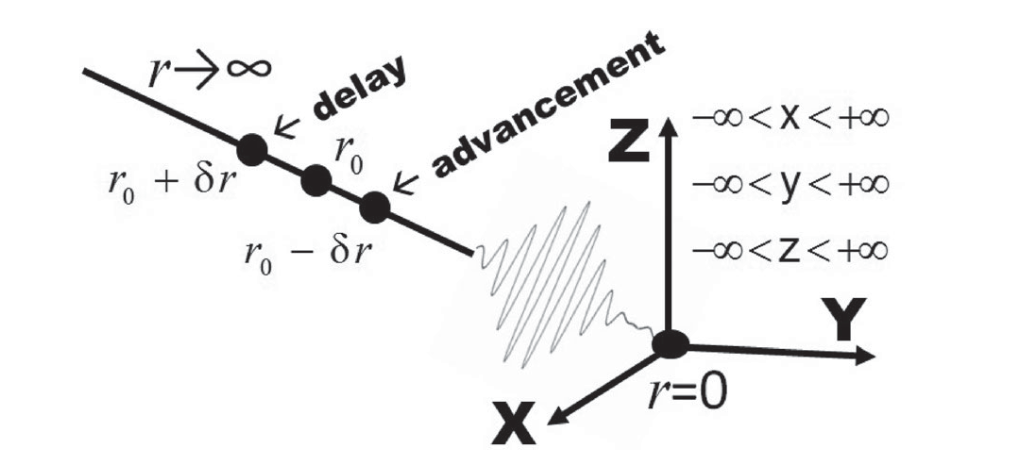
波包起源于远离散射中心的位置，然后接近以为中心的散射区。散射后，散射波会再一次远离，趋向于。在散射区内，粒子会停留一段时间，在此期间它与散射势相互作用，导致相对于未受到散射的波包，散射波包将产生时间延迟。由于散射区中的时间延迟，探测器会认为波包是从而不是开始的。因此，观察者会从探测器的记录得出结论，认为波包比实际更远的地方开始其旅程。如果相互作用是排斥性的，导致散射波包被推出，则散射波包会更早到达探测器，并且在探测器看来就像是波包从靠近散射中心的地方开始，如。这对应于“时间提前”而不是“时间延迟”，通常被称为“负时间延迟”。因此，散射波包相对于未散射的波包发生相移，具体是超前或落后取决于势是否是排斥性或吸引性的。

在以散射势中心为原点的球坐标系统中，薛定谔方程的解可写为：

$\psi_\ell(r, t) = e^{-iEt/\hbar} R_\ell(r) Y_\ell^m(r̂) = e^{-i\omega t} R_\ell(r) Y_\ell^m(r̂)$

其中是径向波函数，表示球谐函数，因子表示稳态量子态的动态相位。薛定谔方程的一般解可以写为基对（, ）的叠加。波前由恒定相位的曲面表示：

$\delta(\pm kr - \omega t) = 0.$

因此，

$\frac{\delta r}{\delta t} = \pm \frac{\omega}{k},$

对于向外的波 () 以及向内的波 () 分别为正或负。

将径向波函数表示为：

$R_\ell = \frac{u_\ell}{r},$

径向微分方程的解可以表示为基对的线性叠加，它可以通过递归关系从获得。对于无势散射情况，很容易看出：

$\{u_{\ell=0}^+(r), u_{\ell=0}^-(r)\}_{V=0} = \{e^{+ikr}, e^{-ikr}\}$

的部分波是正弦函数，其自变量是而不是。对于由球贝塞尔函数的叠加表示的入射平面波：

$e^{ik·r} = e^{ikr\cos\theta} = \sum_{\ell=0}^{\infty} i^\ell(2\ell + 1) P_\ell(\cos\theta) j_\ell(kr)$

散射问题的解由著名的表达式给出：

$\psi_{\boldsymbol{k}}^{\text {total }}(\boldsymbol{r}) \underset{r \rightarrow \infty}{\longrightarrow} \mathrm{e}^{\mathrm{i} \boldsymbol{k} \cdot \boldsymbol{r}}+f(\boldsymbol{k}, \hat{\boldsymbol{\Omega}})\left(\mathrm{e}^{\mathrm{i} k r} / r\right)$

其中散射幅由 Faxen–Holtzmark 关系给出：

$f(\boldsymbol{k}, \hat{\boldsymbol{\Omega}}) = \frac{1}{2ik} \sum_{\ell=0}^{\infty} (2\ell + 1) \left[e^{2i\delta_\ell(k)} - 1\right] P_\ell(\cos\theta)$

向外波的相移为，相移为每次入射和远离目标时各自。因此，散射解可以用来表示，其中：

$\phi_{in, \ell} = A u_\ell^-(r)$ $\phi_{out, \ell} = A e^{2i\delta_\ell(k)} u_\ell^+(r)$

如前所述，入射粒子的传播必须用一个围绕动量扩展的波包来表示，而不能用单个单色波。对应于阶部分波的入射波包为：

$\Psi_{b,\ell}(r,t) = \frac{1}{(2\pi)^{3/2}} \int\int\int d^3k \left[A_\ell(k) e^{i(k·(r-b)-\omega(k)t)}\right]$

其中波包从位于散射中心以外的参数开始。

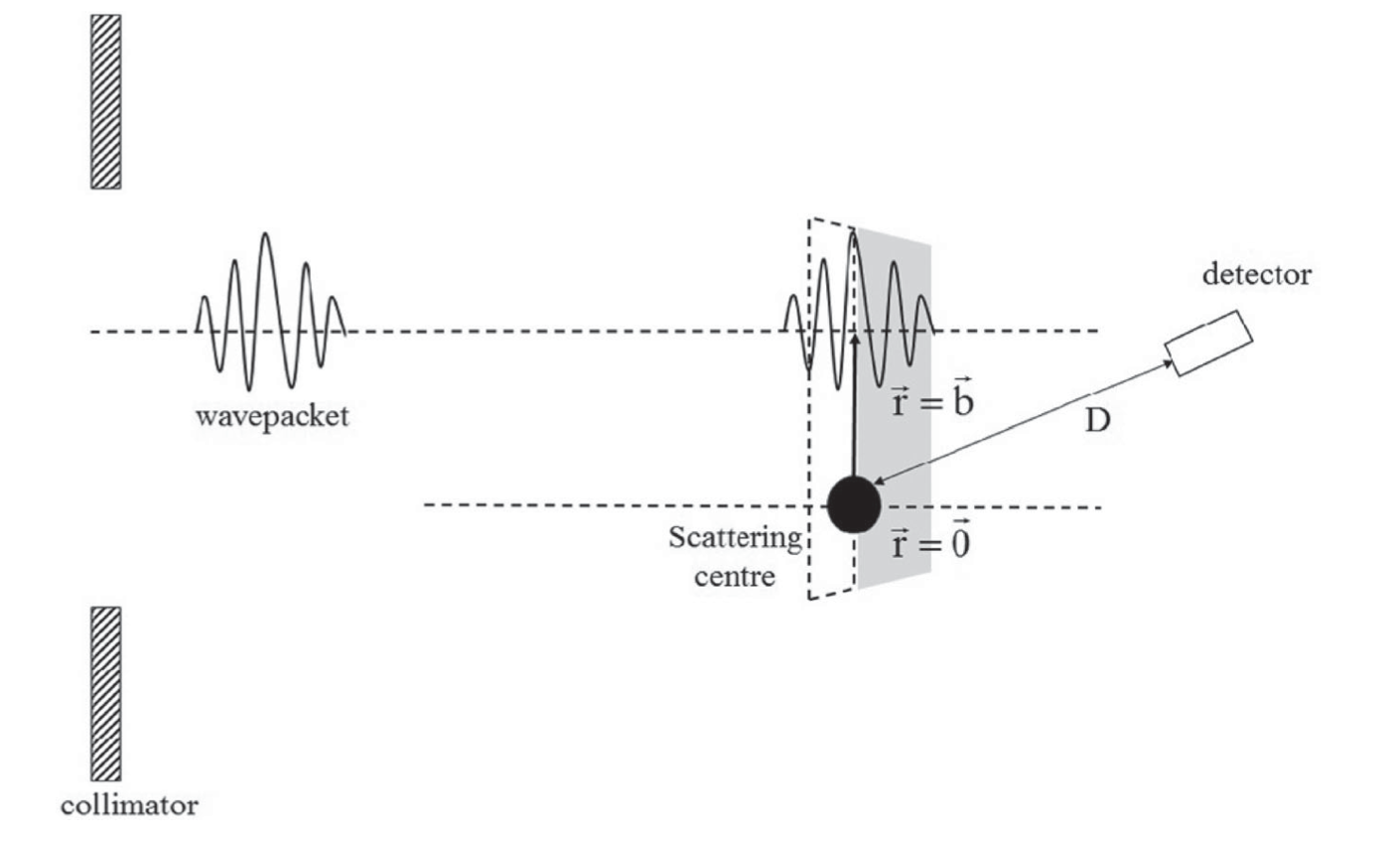
将复系数分为振幅和相位：

$\Psi_{\boldsymbol{b},\ell}(\boldsymbol{r},t) = \frac{1}{(2\pi)^{3/2}} \int\int\int d^3\boldsymbol{k} \left[|A_\ell(\boldsymbol{k})| e^{i(\boldsymbol{k}·(\boldsymbol{r}-\boldsymbol{b})-\omega(\boldsymbol{k})t+\alpha(\boldsymbol{k}))}\right]$

积分中相位的总动量依赖性为：

$\beta(\boldsymbol{k}) = \boldsymbol{k}·(\boldsymbol{r}-\boldsymbol{b}) - \omega(\boldsymbol{k})t + \alpha(\boldsymbol{k})$

波包的位置可以由以下条件定出：

$[\nabla_k \beta(\boldsymbol{k})]_{\boldsymbol{k}=\boldsymbol{k}_0} = 0$

该关系在满足以下条件时成立：

$\boldsymbol{r} = \boldsymbol{v}_g t + \boldsymbol{r}_0 + \boldsymbol{b},$

其中：

$\boldsymbol{v}_g = [\nabla_{k} \omega(\boldsymbol{k})]_{\boldsymbol{k}=\boldsymbol{k}_0}$ $\boldsymbol{r}_0 = -[\nabla_k \alpha(\boldsymbol{k})]_{\boldsymbol{k}=\boldsymbol{k}_0}$

群速度在方向上的分量为：

$v_g = (\boldsymbol{v}_g · \hat{\boldsymbol{k}_0}) = [\nabla_k \omega(\boldsymbol{k})]_{\boldsymbol{k}=\boldsymbol{k}_0} · \hat{\boldsymbol{k}_0} = \left(\frac{d\omega}{dk}\right)_{k=k_0}$

位移矢量在相同方向上的分量为：

$r_{0k_0} = \boldsymbol{r}_0 · \hat{\boldsymbol{k}_0}$

由于垂直于，沿着方向传播的波包中心的瞬时位置为：

$r(t) = (\boldsymbol{v_g} · \hat{\boldsymbol{k}_0}) t + (\boldsymbol{r}_0 · \hat{\boldsymbol{k}_0}) + (\boldsymbol{b} · \hat{\boldsymbol{k}_0}) = v_g t + r_{0k_0}$

方程 (27) 表示波包中心沿方向的传播。

现在我们来看看在波包被散射时方程 (27) 如何变化。我们用上标 “+” 表示散射问题中具有向外波边界条件的解：

$\Psi_{\boldsymbol{b}, \ell}^{+}(\boldsymbol{r}, t) \underset{r \rightarrow \infty}{\longrightarrow} \Phi_{\boldsymbol{b}, \ell}(\boldsymbol{r}, t)+\iiint \frac{\mathrm{d}^3 \boldsymbol{k}}{(2 \pi)^{3 / 2}}\left[A_{\ell}(\boldsymbol{k}) \mathrm{e}^{-\mathrm{i} \boldsymbol{k} \cdot \boldsymbol{b}} f_{\ell}(\boldsymbol{k}, \hat{\boldsymbol{\Omega}}) \frac{\mathrm{e}^{\mathrm{i}\{k \boldsymbol{r}-\omega(\boldsymbol{k}) t\}}}{r}\right],$

其中是散射幅。

将复散射幅分为其大小和相位，散射部分（用上标 “s” 表示）的波函数为：

$\Psi_{\boldsymbol{b}, \ell}^{\mathrm{s}}(\boldsymbol{r}, t) \underset{r \rightarrow \infty}{\longrightarrow} \iiint \frac{\mathrm{~d}^3 \boldsymbol{k}}{(2 \pi)^{3 / 2}}\left[\left|A_{\ell}(\boldsymbol{k})\right| \left| f_{\ell}\left(\boldsymbol{k}_0, \hat{\boldsymbol{\Omega}}\right)\right| \frac{\mathrm{e}^{\mathrm{i}\left\{k r-\omega(\boldsymbol{k}) t+\alpha(\boldsymbol{k})+\Lambda_{\ell}(\boldsymbol{k}, \hat{\boldsymbol{\Omega}})-\boldsymbol{k} \cdot \boldsymbol{b}\right\}}}{r}\right]$

每个动量成分的相位为：

$\xi_\ell(\boldsymbol{k}) = kr - \omega(\boldsymbol{k})t + \alpha(\boldsymbol{k}) + \Lambda_{\ell}(\boldsymbol{k}, \hat{\boldsymbol{\Omega}}) - \boldsymbol{k}·\boldsymbol{b}$

驻相条件，如方程 (21) 所示，现在为：

$[\nabla_k \xi_\ell(\boldsymbol{k})]_{\boldsymbol{k}=\boldsymbol{k}_0} = 0$

该条件在以下情况下成立：

$r\hat{\boldsymbol{k}_0} - [\nabla_k \omega(\boldsymbol{k})]_{\boldsymbol{k}=\boldsymbol{k}_0} t + [\nabla_k \alpha(\boldsymbol{k})]_{\boldsymbol{k}=\boldsymbol{k}_0} + [\nabla_k \Lambda_{\ell}(\boldsymbol{k})]_{\boldsymbol{k}=\boldsymbol{k}_0} - \boldsymbol{b} = 0,$

即：

$r\hat{\boldsymbol{k}_0} - \boldsymbol{v}_g t - \boldsymbol{r}_0 + \boldsymbol{\rho}_\ell(\hat{\boldsymbol{\Omega}}) - \boldsymbol{b} = 0,$

其中：

$\boldsymbol{\rho}_\ell(\hat{\boldsymbol{\Omega}}) = [\nabla_k \Lambda_{\ell}(\boldsymbol{k})]_{\boldsymbol{k}=\boldsymbol{k}_0}$

这给出了沿方向传播的波包中心的瞬时位置：

$r(t) = v_g t + r_{0k_0} - (\boldsymbol{\rho}_\ell · \hat{\boldsymbol{k}_0})$

比较方程 (27) 和方程 (35)，我们可以看到入射粒子的波包与散射势相互作用导致了一个空间偏移。这个空间偏移与群速度的比值对应于波包在通过相互作用区域时的时间延迟，称为 Wigner-Eisenbud 时间延迟：

$\tau_{Wigner \, Eisenbud} = \frac{[\boldsymbol{\rho}_\ell(\hat{\boldsymbol{\Omega}}) · \hat{\boldsymbol{k}_0}]}{v_g}$

由于是相位角在处的动量空间梯度，其在方向上的分量就是相角对的方向导数：

$\tau_{Wigner \, Eisenbud} = \frac{\frac{d\Lambda_{\ell}}{dk}}{\frac{d\omega}{dk}} \bigg|_{k=k_0} = \hbar \frac{d\Lambda_{\ell}}{dE} \bigg|_{E=E_0} = \hbar \left( \frac{d}{dE} \left\{ \arg f_{\ell}\left(\boldsymbol{k}, \hat{\boldsymbol{\Omega}}\right) \right\} \right) \bigg|_{E=E_0}$

由于是复散射幅的相位角，方程 (23b) 表示量子散射中的时间延迟是散射相位对能量的导数。通常称为 Wigner 时间延迟或 Wigner-Eisenbud 时间延迟。