非线性光学导论I
非线性光学导论I
本文参考文章Introduction to nonlinear optics
目录
- 什么是非线性效应以及为什么会发生非线性效应
- 介质中的麦克斯韦方程组
- 非线性光学介质
- 二次谐波
- 光子的守恒定律(Phase Match)
什么是非线性效应以及为什么会发生非线性效应
什么是非线性效应
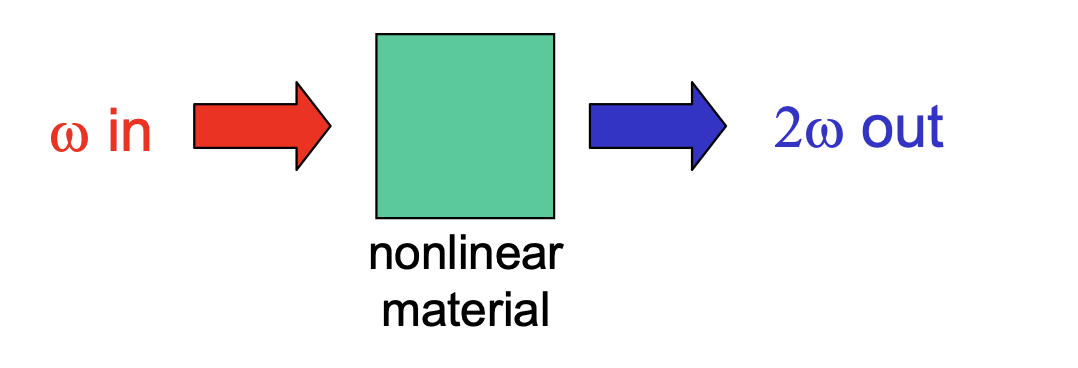
将一束红外光射入一个晶体中会产生绿光:
非线性光学可以改变一束光的颜色、空间和时间上的分布或者人为产生超快过程。
非线性光学现象是许多光学器件(例如光通信设备、光传感器)的重要原理
为什么会发生非线性效应
入射光会与介质分子发生相互作用,使得介质分子发生振动并发出辐射,辐射光将与原本的光发生干涉。
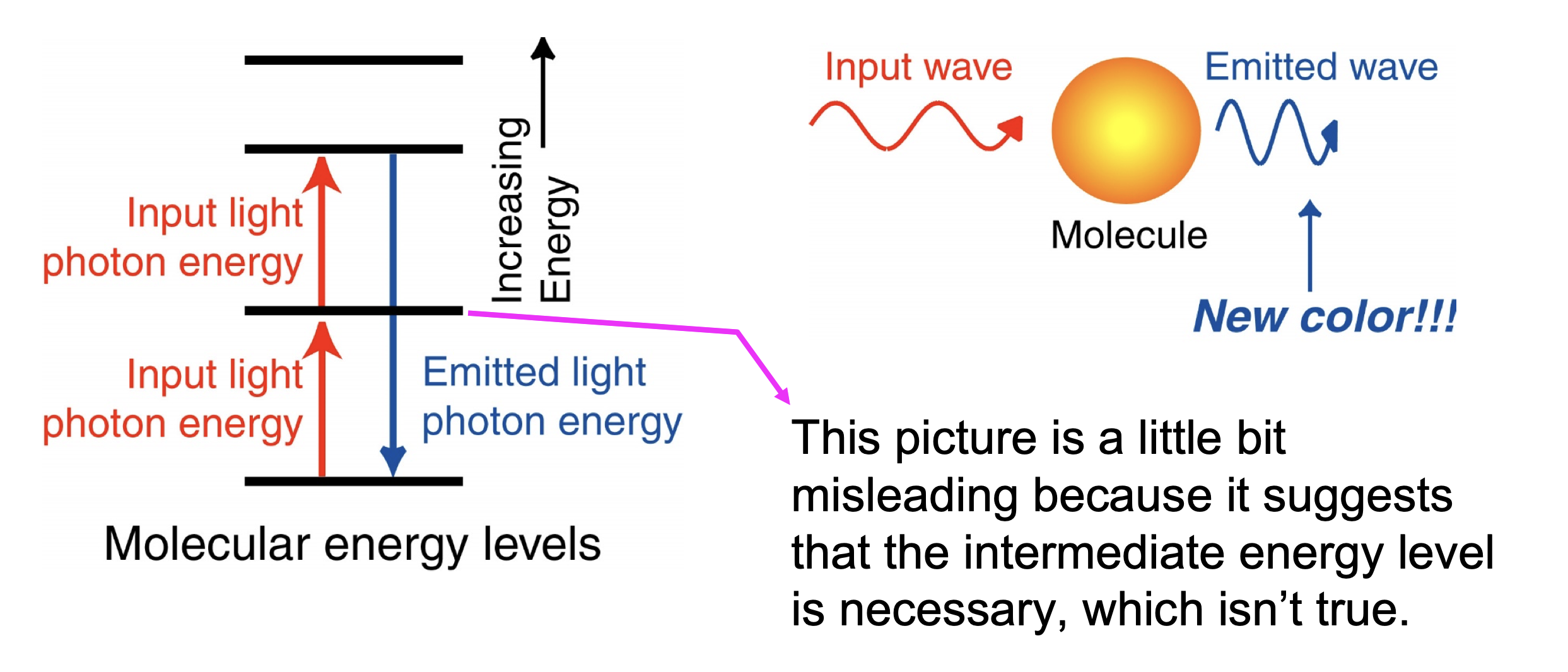
但是当入射光足够强的时候,分子中的电子可以吸收不止一个光子,从而辐射出更高频的光。
需要注意的是吸收多个光子并不需要中间能态
介质中的麦克斯韦方程组
介质中的麦克斯韦方程组可以推导出在介质中的非齐次波动方程:
对于线性介质,极化强度正比于电场强度:
使用有阻尼的受迫振子模型,我们可以得到
如果我们将上述关系带入波动方程,可以得到
我们记介质中的光速为
所以对于一般的线性介质,光在其中传播受到的仅有的影响就是光速由原本的
但是当
非线性光学介质
对于非线性介质,极化强度
此时的波动方程则需写为
具体展开写就是
一般而言,由于
二次谐波
这个时候,如果我们认为电场强度具有形式
那么非线性项就会引入
然后我们惊讶的发现二次谐波产生了!
如果有两束不同的光入射,那么我们预期电场强度有以下部分
那么非线性项就会引入
以及
这样和频和差频就产生了
以上都是从宏观的角度(极化强度)来考察非线性介质所产生的非线性效应,那么从微观的角度来看,我们可以把非线性过程称为
“N-wave-mixing processes”(显然我不知道这该怎么翻译)
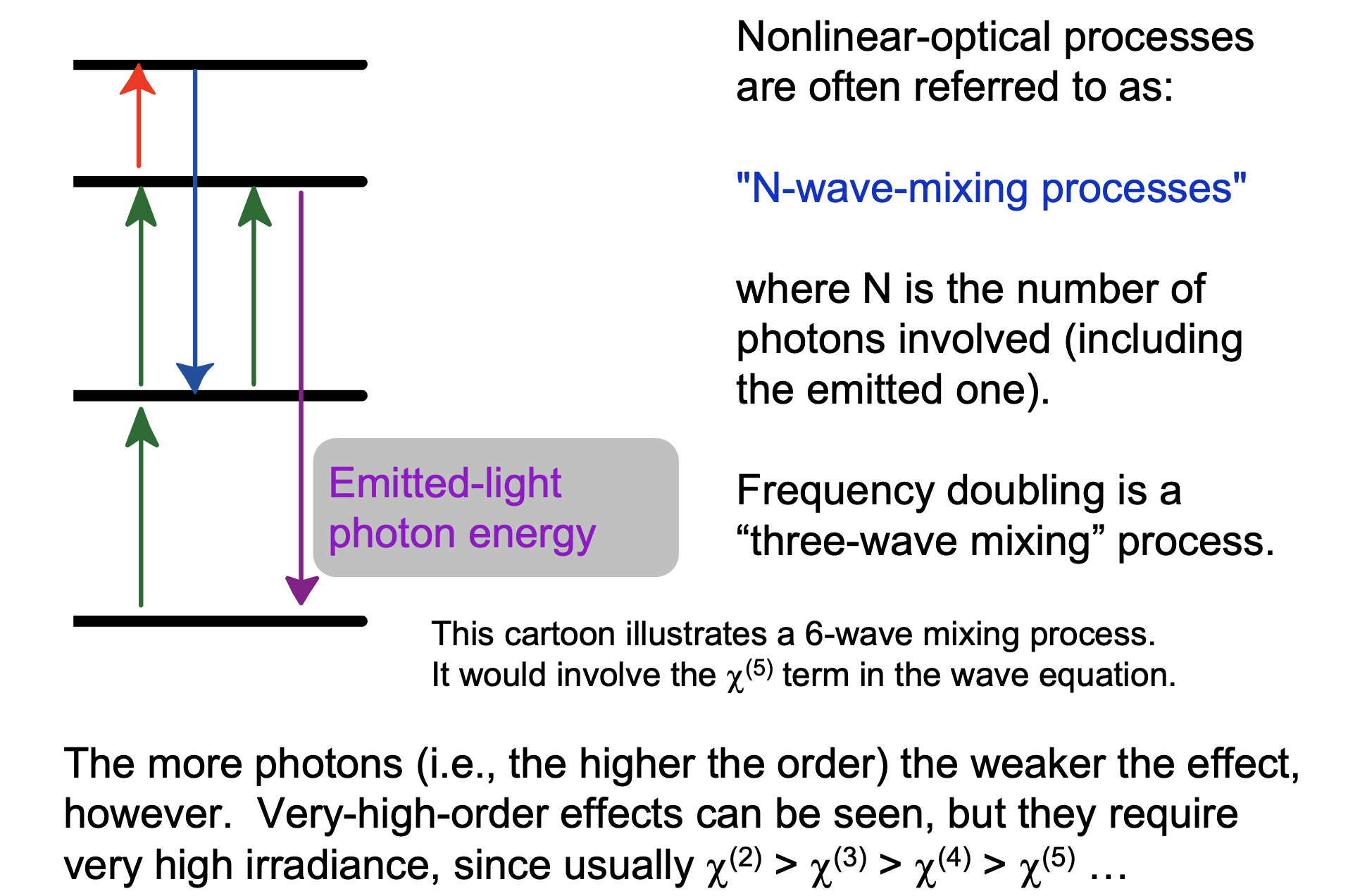
像倍频就是一个“three-wave mixing”过程,而一个“6-wave mixing”过程可以反映到波动方程中
[!CAUTION]
这里有关“N-wave mixing processes”讲得不是很清楚,可以看一下ChatGPT是如何回答:
- N-wave mixing: The term “N” in N-wave mixing refers to the number of waves involved in the process. For example:
- 2-wave mixing is the simplest case, such as in second-harmonic generation (where two photons at a certain frequency combine to produce one photon at twice the frequency).
- 3-wave mixing involves three waves, such as in sum-frequency generation (SFG) or difference-frequency generation (DFG).
- 4-wave mixing is a more common example in nonlinear optics, where four waves interact to produce new frequencies through processes like phase conjugation or frequency shifting.
光子的守恒定律
考虑到光与物质作用完后物质将恢复原本的状态(暂且不考虑介质受损的情况),我们认为光子在入射前后的能量和动量是要守恒的,所以我们有
同时满足上面的条件我们称之为
“phase matching”
[!CAUTION]
我看到很多其他文献好像没有提到第一条能量守恒,不知道为什么
Phase-matching 的一个例子
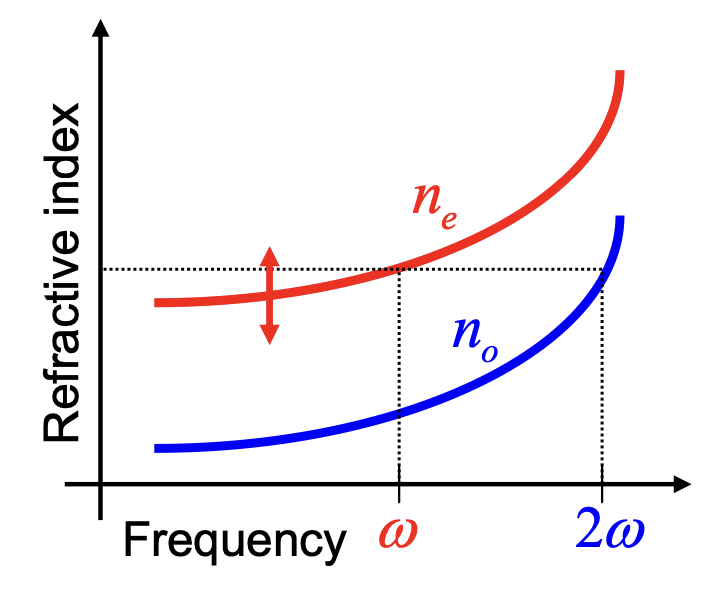
对于动量守恒,我们有
利用关系式
但是想要找到一个折射率不随频率变化的介质是几乎不可能的
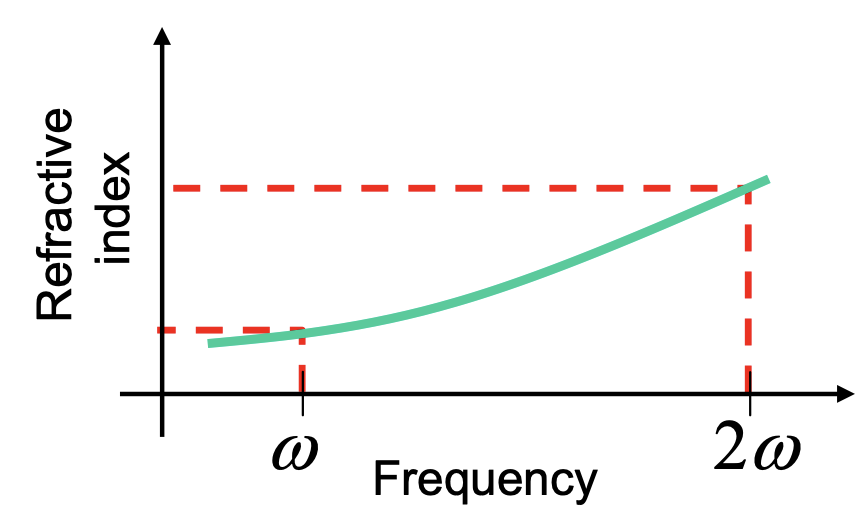
但是我们可以选择有双折射晶体呀,这样我们对于不同偏振方向的光会有不同的折射率,这样就为满足上面的式子提供了一中可能。
更关键的是,我们还可以通过旋转介质的角度来调整折射率